pliref




Next: plrefl
Up: XSPEC V9 Models
Previous: plabs
The total spectrum resulting from a power-law illumination of material of an
arbitrary ionisation state, i.e., the power law together with its reflection
spectrum, calculated self-consistently for ionised material. The reflected
spectrum is calculated following Lightman and White (1988), Ap.J., 335, 57,
but with opacities calculated by solving the Saha equation, balancing
photo-ionisation with recombination. The amount of photo-ionisation is
determined from the ionisation parameter, 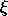 =L/(nR
=L/(nR ), where L is the total
photo-ionising luminosity of the source, assumed to be the power law integrated
between 5eV and 300 keV; n is the density of the illuminated material; and R
is its distance from the X-ray source. Note that this definition of
), where L is the total
photo-ionising luminosity of the source, assumed to be the power law integrated
between 5eV and 300 keV; n is the density of the illuminated material; and R
is its distance from the X-ray source. Note that this definition of 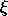 differs
in bandpass from the 13.6eV - 13.6 keV used by Kallman and McCray (1982),
Ap. J. Supp., 50, 263, so that their
differs
in bandpass from the 13.6eV - 13.6 keV used by Kallman and McCray (1982),
Ap. J. Supp., 50, 263, so that their 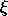 is around an order of
magnitude less
than that used here. The recombination rate is dependent on the temperature
of the material: the approximations used here are generally valid between
1e3 and 1e6 K. Photo-ionisation cross-sections are taken from Reilman and
Manson (1979), Ap. J. Supp., 40, 815, recombination coefficients from Shull and
Van Steenburg (1982), Ap. J. Supp., 48, 95, and abundances from Lang (1974),
Astrophysical Formulae.
is around an order of
magnitude less
than that used here. The recombination rate is dependent on the temperature
of the material: the approximations used here are generally valid between
1e3 and 1e6 K. Photo-ionisation cross-sections are taken from Reilman and
Manson (1979), Ap. J. Supp., 40, 815, recombination coefficients from Shull and
Van Steenburg (1982), Ap. J. Supp., 48, 95, and abundances from Lang (1974),
Astrophysical Formulae.
The reflected spectrum is assumed to scale as the cosine of the inclination
angle. This is not a bad approximation at small angles, but is increasingly
inaccurate at large inclinations, especially as doppler effects are not
included in this code. See George and Fabian (1991), M.N.R.A.S., 249, 352;
and Matt, Perola and Piro (1991), Astron. Astrophys., 247, 25 for more
accurate calculations of inclination effects. As Compton down-scattering is
important, the X-ray spectrum beyond the 2-20 keV band can affect the
calculated shape of the reflection spectrum. The recommended maximum energy
cut-off is 0.6 (= 300 keV). See Done et al., (1992) Ap. J., 395, 275 for more
details and an example of use.





Next: plrefl
Up: XSPEC V9 Models
Previous: plabs
Keith Arnaud (kaa@genji.gsfc.nasa.gov)
Mon Sep 18 14:36:38 EDT 1995
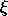 =L/(nR
=L/(nR ), where L is the total
photo-ionising luminosity of the source, assumed to be the power law integrated
between 5eV and 300 keV; n is the density of the illuminated material; and R
is its distance from the X-ray source. Note that this definition of
), where L is the total
photo-ionising luminosity of the source, assumed to be the power law integrated
between 5eV and 300 keV; n is the density of the illuminated material; and R
is its distance from the X-ray source. Note that this definition of 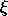 differs
in bandpass from the 13.6eV - 13.6 keV used by Kallman and McCray (1982),
Ap. J. Supp., 50, 263, so that their
differs
in bandpass from the 13.6eV - 13.6 keV used by Kallman and McCray (1982),
Ap. J. Supp., 50, 263, so that their 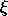 is around an order of
magnitude less
than that used here. The recombination rate is dependent on the temperature
of the material: the approximations used here are generally valid between
1e3 and 1e6 K. Photo-ionisation cross-sections are taken from Reilman and
Manson (1979), Ap. J. Supp., 40, 815, recombination coefficients from Shull and
Van Steenburg (1982), Ap. J. Supp., 48, 95, and abundances from Lang (1974),
Astrophysical Formulae.
is around an order of
magnitude less
than that used here. The recombination rate is dependent on the temperature
of the material: the approximations used here are generally valid between
1e3 and 1e6 K. Photo-ionisation cross-sections are taken from Reilman and
Manson (1979), Ap. J. Supp., 40, 815, recombination coefficients from Shull and
Van Steenburg (1982), Ap. J. Supp., 48, 95, and abundances from Lang (1974),
Astrophysical Formulae.
