Cash (ApJ 228, 939) showed that the 
minimization
criterion is a very bad one if any of the observed data bins
had few counts. A better criterion is to use a likelihood function :
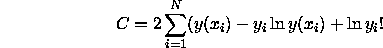
where 
are the observed data and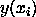 
the values of the function.
Minimizing C for some model gives the best-fit parameters.
Furthermore, this statistic can be used in the same, familiar way as
the statistic
to find confidence intervals. One finds the parameter values that give
, where N is the same number that gives the required
confidence
for the number of interesting parameters as for the case.
Castor (priv. comm.) has pointed out that a better function to use is :
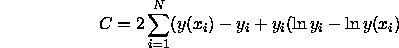
This differs from the first function by a quantity that depends only
upon the data. This second function does provide a goodness-of-fit
criterion similar to that of and it is now used in XSPEC. It
is important to note that the C-statistic assumes that the error on
the counts is pure Poisson, and thus it cannot deal with data that
already has been background subtracted, or has systematic errors.