Using XSPEC to Simulate Data: an Example from ASCA




Next: Producing Plots: Modifying
Up: Walks through XSPEC
Previous: Fitting Data Files
In several cases, analyzing simulated data is a powerful tool to
demonstrate feasibility. For example:
- To support an observing proposal. That is, to demonstrate
what constraints a proposed observation would yield.
- To support a hardware proposal. If a response matrix is
generated, it can be used to demonstrate what kind of science could be
done with a new instrument.
- To support a theoretical paper. A theorist could write a
paper describing a model, and then show how these model spectra would
appear when observed. This, of course, is very like the first case.
Here, we'll use XSPEC to see how an ASCA observation of the
elliptical galaxy NGC 4472 can constrain the condition of the hot gas.
The first step is to define a model on which to base the simulation.
The way XSPEC creates simulated data is to take the current model,
convolve it with the current response matrix, while adding noise
appropriate to the integration time specified. Once created, the
simulated data can be analyzed in the same way as real data to derive
confidence limits.
We begin by looking in the literature for the best estimate of the NGC
4472 spectrum. BBXRT observed the galaxy in 1990 and the results were
published in Serlemitsos et al., (1993). They found a flux in the
0.5-4.5 keV range of  erg cm
erg cm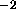 s
s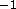 , a
temperature range of
, a
temperature range of 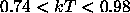 , an abundance range (as a
fraction of solar) of
, an abundance range (as a
fraction of solar) of 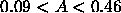 and a column range of
and a column range of  cm
cm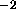 . A Raymond-Smith spectral
model was found to give a good fit. We specify this model at first with
the median parameter values, except for the normalization of the
Raymond-Smith, which we leave at its default value of unity at first (but
adjust later):
. A Raymond-Smith spectral
model was found to give a good fit. We specify this model at first with
the median parameter values, except for the normalization of the
Raymond-Smith, which we leave at its default value of unity at first (but
adjust later):
mo = wabs[1] (raymond[2])
XSPEC> mo wa ray
Input parameter value, delta, min, bot, top, and max values for ...
Mod parameter 1 of component 1 wabs nH 10^22
1.000 1.0000E-03 0. 0. 1.0000E+05 1.0000E+06
0.21
Mod parameter 2 of component 2 raymond kT(keV)
1.000 1.0000E-02 8.0000E-03 8.0000E-03 64.00 64.00
0.86
Mod parameter 3 of component 2 raymond Abundanc
1.000 -1.0000E-03 0. 0. 5.000 5.000
0.27
Mod parameter 4 of component 2 raymond Redshift
0. -1.0000E-03 0. 0. 2.000 2.000
Mod parameter 5 of component 2 raymond norm
1.000 1.0000E-03 0. 0. 1.0000E+05 1.0000E+06
---------------------------------------------------------------------------
---------------------------------------------------------------------------
mo = wabs[1] (raymond[2])
Model Fit Model Component Parameter Value
par par comp
1 1 1 wabs nH 10^22 0.210000 +/- 0.
2 2 2 raymond kT(keV) 0.860000 +/- 0.
3 3 2 raymond Abundanc 0.270000 frozen
4 4 2 raymond Redshift 0. frozen
5 5 2 raymond norm 1.00000 +/- 0.
---------------------------------------------------------------------------
---------------------------------------------------------------------------
3 variable fit parameters
We now can derive the correct normalization by using the commands dummyrsp,
flux and newpar. That is, we'll determine the
flux of the model with the normalization of unity (this requires a
response matrix to cover the BBXRT band-we use a dummy response
here). We then work out the new normalization and reset it:
XSPEC> dummy 0.5 4.5
XSPEC> flux 0.5 4.5
Model flux 0.2912 photons (5.1221E-10 ergs)cm**-2 s**-1 ( 0.500- 4.500)
XSPEC> newpar 5 0.013
3 variable fit parameters
XSPEC> flux
Model flux 3.7860E-03 photons (6.6587E-12 ergs)cm**-2 s**-1 ( 0.500- 4.500)
Here, we have changed the value of the normalization (the fifth
parameter) from 1 to 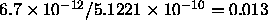 to give the flux observed by BBXRT (
to give the flux observed by BBXRT ( erg cm
erg cm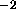 s
s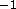 in the energy range 0.5-4.5).
in the energy range 0.5-4.5).
The next stage, creating the simulated data, requires a response matrix.
In this example, we'll use the pre-flight ASCA SIS matrix, sis_small.rmf.
The simulation is initiated with the command
fakeit. If the argument none is given, the user will be prompted
for the name of the response matrix. If no argument is given, the
current response will be used:
XSPEC> fakeit none
For fake data, file # 1 needs response file: sis_small.rmf
There then follows a series of prompts asking the user to specify
whether he or she wants counting statistics (yes!), the name of the fake
data file (ngc4472_sis.fak in our example), and the integration
time T (40,000 seconds-the other quantities A, Bkg,
cornorm can be left at their default values).
Use counting statistics in creating fake data? (y)
Input optional fake file prefix (max 12 chars):
Override default values for file # 1
Fake data filename (sis_small.fak): ngc4472_sis.fak
T, A, Bkg, cornorm ( 1.0000 , 1.0000 , 1.0000 , 0. ): 40000
Net count rate (cts/cm^2/s) for file 1 0.4010 +/- 3.1747E-03
Chi-Squared = 198.2 using 256 PHA bins.
Reduced chi-squared = 0.7835
We now have created a file containing a simulated spectrum of NGC 4472.
As is usual before fitting, we need to check which channels to ignore.
This time, we'll examine the actual numbers of counts in each channel
and reject those that have fewer than 20 per channel. We use iplot counts
and see that our criterion requires us to ignore channels 1-20 and 101-256:
XSPEC> ign 1-20 101-256
Chi-Squared = 74.79 using 80 PHA bins.
Reduced chi-squared = 0.9713
As expected,  is excellent even before fitting because the
model and the data have the same shape. But the point of this simulation
is to determine confidence ranges. First, we thaw the value of the
abundance (fixed by default), fit and then use the error command:
is excellent even before fitting because the
model and the data have the same shape. But the point of this simulation
is to determine confidence ranges. First, we thaw the value of the
abundance (fixed by default), fit and then use the error command:
XSPEC> thaw 3
Number of variable fit parameters = 4
XSPEC> fit
Chi-Squared Lvl Fit param # 1 2 3 4
5
69.395 -3 0.2236 0.8557 0.2607 0.
1.3502E-02
69.355 -4 0.2238 0.8554 0.2604 0.
1.3536E-02
69.355 3 0.2238 0.8554 0.2604 0.
1.3536E-02
---------------------------------------------------------------------------
---------------------------------------------------------------------------
mo = wabs[1] (raymond[2])
Model Fit Model Component Parameter Value
par par comp
1 1 1 wabs nH 10^22 0.223845 +/- 0.85826E-02
2 2 2 raymond kT(keV) 0.855436 +/- 0.42361E-02
3 3 2 raymond Abundanc 0.260423 +/- 0.12511E-01
4 4 2 raymond Redshift 0. frozen
5 5 2 raymond norm 1.353650E-02 +/- 0.45268E-03
---------------------------------------------------------------------------
---------------------------------------------------------------------------
Chi-Squared = 69.35 using 80 PHA bins.
Reduced chi-squared = 0.9126
XSPEC> err 1 2 3
Fit Index Confidence Range ( 2.706)
1 0.210177 0.238260
2 0.848311 0.862247
3 0.240804 0.282047
These confidence ranges show that an ASCA observation would
definitely constrain the parameters, especially the column and
abundance, more tightly than the original BBXRT observation. Of
course, whether these constraints are sufficient depends on the theories
being tested. When producing and analyzing simulated data, it is crucial
to keep in mind the purpose of the proposed observation, for the
potential parameter space that can be covered with simulations is almost
limitless.




Next: Producing Plots: Modifying
Up: Walks through XSPEC
Previous: Fitting Data Files
Keith Arnaud (kaa@genji.gsfc.nasa.gov)
Mon Sep 18 14:36:38 EDT 1995
 erg cm
erg cm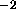 s
s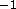 , a
temperature range of
, a
temperature range of 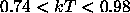 , an abundance range (as a
fraction of solar) of
, an abundance range (as a
fraction of solar) of 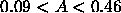 and a column range of
and a column range of  cm
cm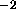 . A Raymond-Smith spectral
model was found to give a good fit. We specify this model at first with
the median parameter values, except for the normalization of the
Raymond-Smith, which we leave at its default value of unity at first (but
adjust later):
. A Raymond-Smith spectral
model was found to give a good fit. We specify this model at first with
the median parameter values, except for the normalization of the
Raymond-Smith, which we leave at its default value of unity at first (but
adjust later):
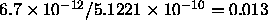 to give the flux observed by BBXRT (
to give the flux observed by BBXRT ( is excellent even before fitting because the
model and the data have the same shape. But the point of this simulation
is to determine confidence ranges. First, we thaw the value of the
abundance (fixed by default), fit and then use the error command:
is excellent even before fitting because the
model and the data have the same shape. But the point of this simulation
is to determine confidence ranges. First, we thaw the value of the
abundance (fixed by default), fit and then use the error command: